Abstract Generator
We are working on the implementation of a transformer for the purpose of text generation. Our goal is to create a transformer model able to write a full scientific abstract given a short prompt. We train this transformer on a subset of abstracts from the arXiv.
We split our approach into the following categories:
- Data Preparation
- Tokenization
- Architecture Design
- Training
- Text Generation
Our github code can be found here.
Data Preparation and Tokenization
…
Architecture Design
The goal is to build a model which can take a stream of tokens $\{x_1, \ldots, x_t\}$, and returns a vocabulary-length vector $\bf{w}$ which represents the conditional distribution of the next word. We will denote this mapping by $\mathbf{w} \equiv f(\{x_i\})$.
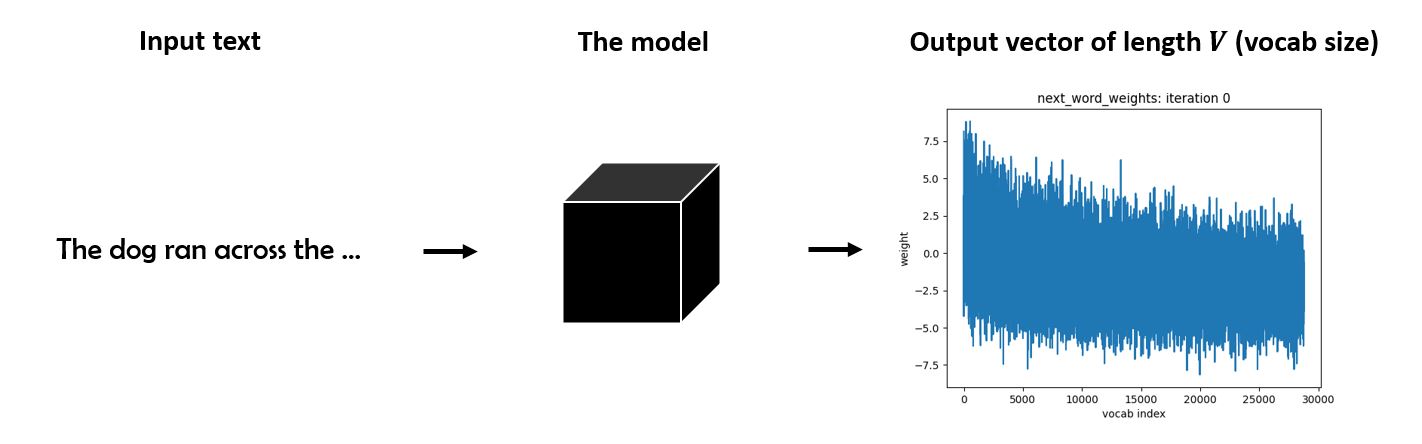
In order to recurrently generate text, the model could in principle feed these prediction vectors back in as input. This idea drove the popularity of recurrent architecutres such as LSTMs for text generation and related tasks.
However, non-recurrent architectures known as Transformers have recently demonstrated good results on various NLP tasks. We have opted to use a Transformer-like architecture for this project.
Training
We used two approaches: SGD and Adam.
- For SGD we tried both monotonic and cylic learning rate schedules (to explore different minima).
- For Adam we specifically used a variation with weight-decay – AdamW.
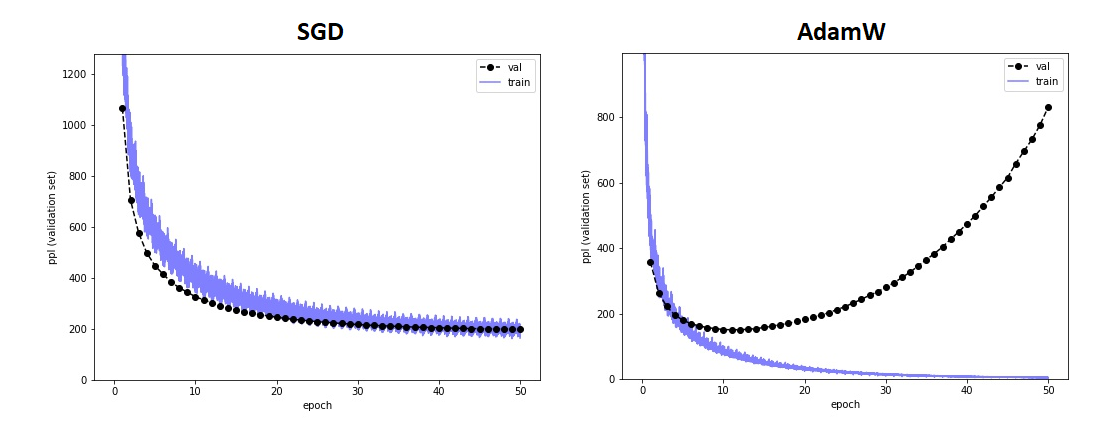
Remarks:
- Both schemes train within a few hours on a single desktop GPU (~3 minutes per epoch).
- Note that while AdamW trains faster, it also overfits rapidly, as indicated by the diverging validation loss.
- SGD training is slower, but is not as prone to overfitting.
Text Generation
Given an input stream of tokens $\{x_1, \ldots, x_t\}$ with some context length $t$, the network will return a vector $\mathbf{w}=f(\{x_i\})$ of length $V$.
A naive approach to text generation is “greedy decoding” - just keep selecting the token with the largest weight, $x_{t+1} = \underset{i\in V}{\operatorname{argmax}} \bf{w}$. Unfortunately, this naive scheme often gets stuck repeating certain words or phrases depending on the initial condition and context length.
A more flexible approach is to contruct a boltzmann distribution from the weights $\bf{w}$, and sample from that. Note that this distribution is what the transformer is attempting to fit during training. We now have an explicit probability vector $\bf{p}$ for the next-word distribution.
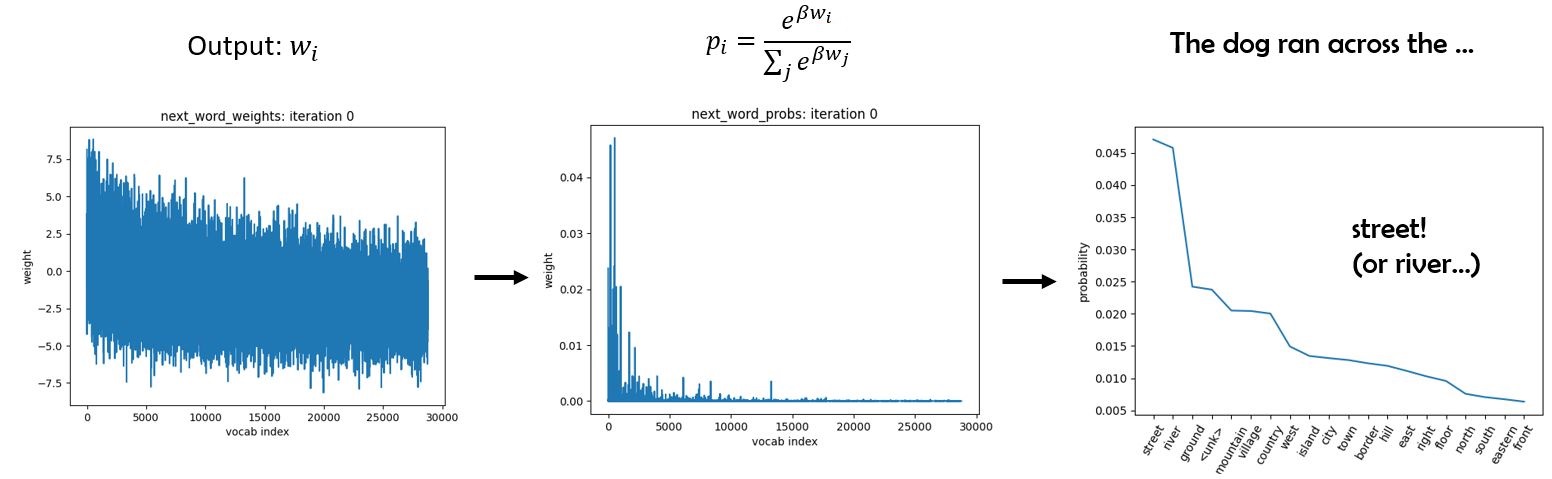
Note that this introduces a hyperparameter $\beta$ which is sometimes called the inverse-temperature parameter. Why? As $\beta \rightarrow 0$ everything “melts”, with $\bf{p}$ limiting to a uniform distribution over the vocabulary. On the other hand, when $\beta \rightarrow \infty$, $\bf{p}$ becomes sharply peaked at the most probable word, recovering greedy decoding. The plot above shows $\beta=1$. Using intermediate $\beta$ allows us to generate much more natural text: loops become rare and unusual words have a chance to appear.